 | |
Signals are made up of sine waves. Sometimes just one, as in the diagram, and sometimes of several that have frequencies that are whole-number multiples of the basic sine wave. These are the basic sine wave's harmonics.
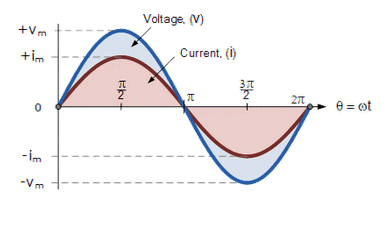
As an alternating quantity, sine waves have a positive maximum value at time π / 2, a negative maximum value at time 3π / 2, with zero values occurring along the baseline at 0, π and 2π.
When sinusoidal waveforms do not pass exactly through the zero axis point at the same time, they are said to have been "shifted", either to the right or to the left of 0o by some value when compared to another sine wave.
|
For example, when capacitors or inductors are involved in an AC circuit, the current and voltage do not peak at the same time, so they form the basics of phase shift circuits. The fraction of a period difference between the peaks expressed in degrees is said to be the phase difference. The phase vector or phasor is used to represent the behaviour of sine waves in circuits and phase effects.
- The phase difference is ≤ 90 degrees. It is customary to use the angle by which the voltage leads the current. This leads to a positive phase for inductive circuits since current lags the voltage in an inductive circuit.
| The voltage on a capacitor is directly proportional to the charge on it. The current must lead the voltage in time and phase so as to conduct charge to the capacitor and so raise the voltage.
When a voltage is applied to an inductor it opposes the change in current (back emf effect) . So the current builds up more slowly than the voltage and lags it in time and phase. | |
 |
- The phase difference or phase shift as it is also called is the angle Φ, in degrees or radians that the waveform has shifted from a certain reference point along the horizontal zero axis. In other words phase shift is the lateral difference between two or more waveforms along a common axis and sinusoidal waveforms of the same frequency can have a phase difference.
The phase difference, Φ of an alternating waveform can vary from between 0 to its maximum time period, T of the waveform during one complete cycle and this can be anywhere along the horizontal axis between, Φ = 0 to 2π (radians) or Φ = 0 to 360o depending upon the angular units used.
Phase difference can also be expressed as a time shift of t in seconds representing a fraction of the time period, T for example, +10mS or - 50uS but generally it is more common to express phase difference as an angular measurement.
Then the equation for the instantaneous value of a sinusoidal voltage or current waveform will need to be modified to take account of the phase angle of the waveform and this new general expression becomes.
At = Amax * sin(ωt ± Φ)
Where:



