During this charging process, a charging current, i flows into the capacitor opposed by any changes to the voltage at a rate which is equal to the rate of change of the electrical charge on the plates. A capacitor therefore has an opposition to current flowing onto its plates. The relationship between this charging current and the rate at which the capacitors supply voltage changes can be defined mathematically as:

i = C(

dv / dt

)

• C is the capacitance value of the capacitor in farads and
• dv / dt
  is the rate of change of the supply voltage with respect to time.

In a sinusoidal voltage circuit that contains "AC Capacitance", the capacitor will alternately charge and discharge at a rate determined by the frequency of the supply. Then capacitors in AC circuits are constantly charging and discharging respectively. When an alternating sinusoidal voltage is applied to the plates of an AC capacitor, the capacitor is charged firstly in one direction and then in the opposite direction changing polarity at the same rate as the AC supply voltage. This instantaneous change in voltage across the capacitor is opposed by the fact that it takes a certain amount of time to deposit (or release) this charge onto the plates and is given by V = Q / C . 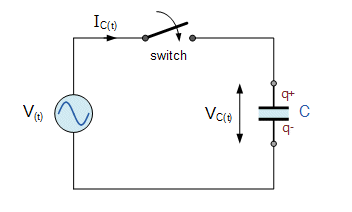Consider the circuit left. When the switch is closed in the circuit, a high current will start to flow into the capacitor as there is no charge on the plates at t = 0. The sinusoidal supply voltage, V is increasing in a positive direction at its maximum rate as it crosses the zero reference axis at an instant in time given as 0o.

As the supply voltage reaches its 90o point on the waveform it begins to slow down and for a very brief instant in time the potential difference across the plates is neither increasing nor decreasing. Therefore the current decreases to zero as there is no rate of voltage change.
At this 90^o point the potential difference across the capacitor is at its maximum ( Vmax ), no current flows into the capacitor as the capacitor is now fully charged and its plates saturated with electrons.

At the end of this instant in time the supply voltage begins to decrease in a negative direction down towards the zero reference line at 180o. Although the supply voltage is still positive in nature the capacitor starts to discharge some of its excess electrons on its plates in an effort to maintain a constant voltage. This results in the capacitor current flowing in the opposite or negative direction. ;

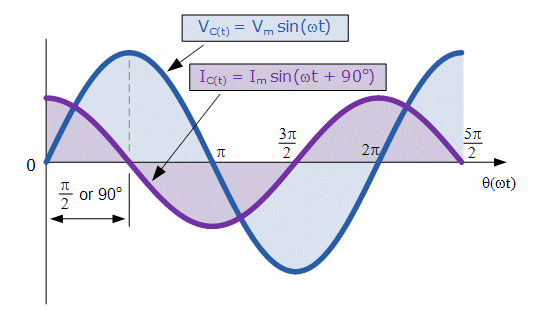When the supply voltage waveform crosses the zero reference axis point at instant 180o the rate of change or slope of the supply voltage is at its maximum but in a negative direction. Consequently the current flowing into the capacitor is also at its maximum rate at that instant. Also at this 180o point the potential difference across the plates is zero as the amount of charge is equally distributed between the two plates. Then, during this first half cycle 0o to 180o, the applied voltage reaches its maximum positive value a quarter of a cycle ( ƒ / 4 ) after the current reaches its maximum positive value. In other words, a voltage applied to a purely capacitive circuit "LAGS" the current by a quarter of a cycle or 90o as shown left.

During the second half cycle 180o to 360o, the supply voltage reverses direction and heads towards its negative peak value at 270^o. At this point the potential difference across the plates is neither decreasing nor increasing and the current decreases to zero.
The potential difference across the capacitor is at its maximum negative value, no current flows into the capacitor and it becomes fully charged the same as at its 90^o point but in the opposite direction.As the negative supply voltage begins to increase in a positive direction towards the 360^o point on the zero reference line, the fully charged capacitor must now loose some of its excess electrons to maintain a constant voltage as before and starts to discharge itself until the supply voltage reaches zero at 360^o at which the process of charging and discharging starts over again.

Unlike a resistor where the opposition to current flow is its actual resistance, the opposition to current flow in a capacitor is called Reactance and, like resistance, reactance is measured in Ohm's Since capacitors charge and discharge in proportion to the rate of voltage change across them, the faster the voltage changes the more current will flow.
Likewise, the slower the voltage changes the less current will flow. This means then that the reactance of an AC capacitor is "inversely proportional" to the frequency of the supply

Z_c =

1 / 2πfC

• Z_c is the Capacitive Reactance in Ohms,
• ƒ is the frequency in Hertz and
• C is the AC capacitance in Farads, symbol F.

In an AC circuit containing pure capacitance the current (electron flow) flowing into the capacitor is given as:

I_C(t) =

dq / dt

where q = CVc = CV_maxsin(ωt)
= C

d V_maxsin(ωt)) / dt

= ωCV_maxcos(ωt)

I_C(t) = I_maxsin(ωt + 90^o)

Whilst in theory the current flowing into a pure AC capacitance leads the voltage by 90o. However, in the real world, it is impossible to have a pure AC Capacitance as all capacitors will have a certain amount of internal resistance across their plates giving rise to a leakage current.
Considering a capacitor as being one that has a resistance, R in series with a capacitance, C producing what can be loosely called an "impure capacitor".

If the capacitor has some "internal" resistance then the total impedance of the capacitor is represented as a resistance in series with a capacitance and in an AC circuit that contains both capacitance, C and resistance, R the voltage phasor, V across the combination will be equal to the phasor sum of the two component voltages, V_R and V_C.
This means then that the current flowing into the capacitor will still lead the voltage, but by an amount less than 90o depending upon the values of R and C giving us a phasor sum with the corresponding phase angle between them given by the Greek symbol phi, φ.

In the RC series circuit left, the current flowing into the circuit is common to both the resistance and capacitance, while the voltage is made up of the two component voltages, VR and VC. The resulting voltage of these two components can be found mathematically but since vectors VR and VC are 90o out-of-phase, they can be added vectorially by constructing a vector diagram. To be able to produce a vector diagram for an AC capacitance a reference or common component must be found. In a series AC circuit the current is common and can therefore be used as the reference source because the same current flows through the resistance and into the capacitance. The individual vector diagrams for a pure resistance and a pure capacitance are given as:

Both the voltage and current vectors for an AC Resistance are in phase with each other. The current leads the voltage ( ICE ) in a pure AC capacitance circuit, therefore the voltage vector VC is drawn 90o behind ( lagging ) the current vector.

In the vector diagram right, line OB represents the horizontal current reference and line OA is the voltage across the resistive component which is in-phase with the current. 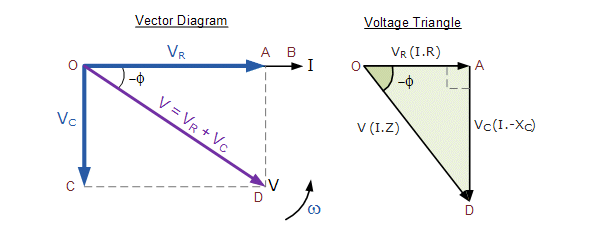Line OC shows the capacitive voltage which is 90o behind the current therefore it can still be seen that the current leads the purely capacitive voltage by 90o. Line OD gives us the resulting supply voltage. As the current leads the voltage in a pure capacitance by 90o the resultant phasor diagram drawn from the individual voltage drops VR and VC represents a right angled voltage triangle shown above as OAD. Pythagoras can be used to find the value of this resultant voltage across the resistor/capacitor ( RC ) circuit.

V² = V_R² + V_C² therefore V² = I² * R² + I² * Z_C². So
V = I * √(R² + Z_C²) and I =

V / √(R² + Z_C²)

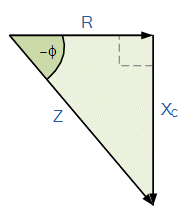>	√(R2 + XC2) represents the impedance, of the circuit. R2 + XC2 represents a right-angle triangle means that by using Pythagoras theorem the negative phase angle, θ between the voltage and current is calculated as. cos θ = R / Z and sin θ = XC / Z