GOOD2USE Knowledge Network PC Phasors

GOOD2USE Knowledge Network PC Phasors

Good Knowledge Is Good2Use

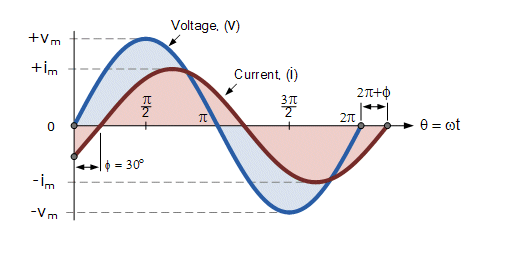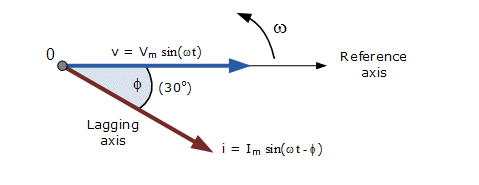A phasor, a combination of the two words phase and vector, is a mathematical means of representing a sinusoidal function with amplitude A, angular frequency (ω), and initial phase (Φ) as are time-invariant. This representation also includes a graphical representation in the form of a phasor diagram, shown left. The vector representation is described by a complex number of the form a + bj, where j is a complex (or imaginary) number equal to √-1, an impossible number hence imaginary.

The top figure showing two sine waves with the current wave (red) lagging the voltage (blue) by Φ in this case 30^o. These two sinusoidal quantities will be written as:

V_t= V_m * sin(ωt) and
I_t = I_m * sin(ωt - Φ)

A sine wave can be represented as a rotating wheel with phase shifted sine waves lagging or leading in the rotation cycle. Each wave being described mathematically by a complex number of the form a + bj, where j is a complex (or imaginary) number equal to √-1, an impossible number hence imaginary.
This vector can be drawn corresponding to time zero ( t = 0 ) on the horizontal axis. The length of the phasor being proportional to the values of the voltage, (V) and the current, (I) at the instant in time that the phasor diagram is drawn.
The current phasor lags the voltage phasor by the angle, Φ, as the two phasors rotate in an anticlockwise direction,, therefore the angle, Φ is also measured in the same ant-iclockwise direction. It is related to a more general concept called analytic representation, which breaks a sinusoid down into the product of a complex constant and a factor that encapsulates the frequency and time dependence. It is related to a more general concept called analytic representation, which breaks a sinusoid down into the product of a complex constant and a factor that encapsulates the frequency and time dependence.

It is common in electrical networks to have multiple sinusoids all with the same frequency, but different amplitudes and phases. The circuit right shows the three main passive components, components incapable of controlling current by means of another electrical signal, of resistors, capacitors and inductors .
The circuit is a RLC one, named after the symbols used to define resistors ®, capacitors © and inductors (L) Since the inductive and capacitive reactance's X_L and X_C are a function of the supply frequency, the sinusoidal response of a series RLC circuit will therefore vary with frequency, ƒ.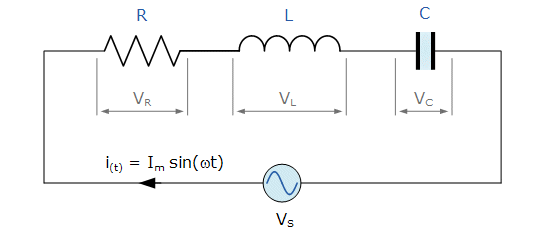

The individual voltage drops across each circuit element of R, L and C element will be "out-of-phase" with each other as defined by:

i(_t) = I_max sin(ωt)

The instantaneous voltage across a pure resistor, V_R is "in-phase" with current
The instantaneous voltage across a pure inductor, V_L"leads" the current by 90^o
The instantaneous voltage across a pure capacitor, V_C "lags" the current by 90^o

Therefore,V_L and V_C are 180^o "out-of-phase" and in opposition to each other.

The amplitude of the source voltage across all three components in a series RLC circuit is made up of the three individual component voltages, V_R, V_L and V_C with the current common to all three components.

The vector diagrams will therefore have the current vector as their reference with the three voltage vectors being plotted with respect to this reference.
This means then that V_R, V_L and V_C cannot simply be added together to find the supply voltage, V_S across all three components as all three voltage vectors point in different directions with regards to the current vector. Therefore it is necessary to find the supply voltage, V_S as the Phasor Sum of the three component voltages combined together vectorially.

The phasor diagram for a series RLC circuit is produced by combining together the three individual phasors and adding these voltages vectorially.
Since the current flowing through the circuit is common to all three circuit elements this can be used as the reference vector with the three voltage vectors drawn relative to this at their corresponding angles.

The resulting vector V_S is obtained by adding together two of the vectors, V_L and V_C and then adding this sum to the remaining vector V_R. The resulting angle obtained between V_S and i will be the circuits phase angle as shown below.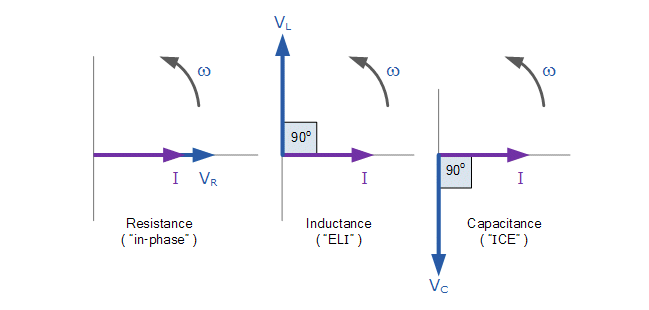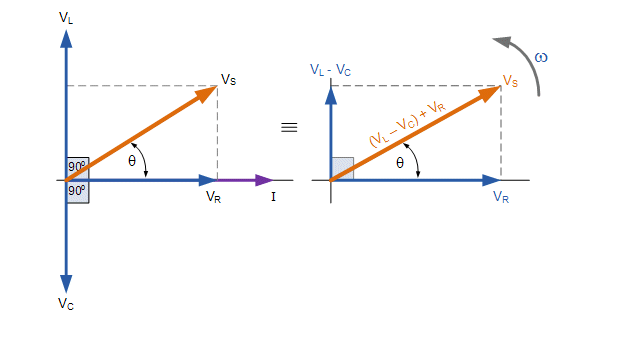

Kirchhoff's voltage law ( KVL ) for both loop and nodal circuits states that around any closed loop the sum of voltage drops around the loop equals the sum of the EMF's. Then applying this law to the these three voltages will give us the amplitude of the source voltage, V_S as.

V_S = V_R + V_L + V_C

Where

V_R is the voltage across the resistor and is a product of the resistance and current
V_L is the voltage across the inductance and is a function of the impedance of the inductance and frequency of the a.c. current
V_C is the vltage across the capacitance and is a function of the impedance of the capacitance and frequency of the a.c. current

V_S = R * I + ωL * I +
I / ωC

Search Knowledge Base

Feedback

If you like our web site refer a friend.
Your friends name.	Your friends email address.
Your Name	Your Email Address