GOOD2USE Knowledge Network PC Impedance

GOOD2USE Knowledge Network PC Impedance

Good Knowledge Is Good2Use

A component in a DC circuit can be described using only its resistance. The resistance of a capacitor in a DC circuit is regarded as an open connection (infinite resistance), while the resistance of an inductor in a DC circuit is regarded as a short connection (zero or very low resistance).
In AC circuits the impedance of an element is a measure of how much the element opposes current flow when an AC voltage is applied across it. It is basically a voltage to current ratio, expressed in terms of frequency. Impedance is treated as complex number, which consists of a real and an imaginary part: The imaginary part, j, represents the effect the frequency of the AC source will have on the component, termed reactance. Resistance in a circuit dissipates power as heat, while reactance stores energy in the form of an electric or magnetic field.
For a resistor in either a DC or AC circuit the voltage across is the resitance value multiplied by the current value - Ohm's Law. It has no imagmary, j, value.

The general term for the impedance (Z) of a component is

Z = R + jX

For a resistor this becomes

Z = R

The impedance of a capacitor is

Z_C =
- j / ωC

where ω is the angular frequency (given by ω = 2πf, where f is the frequency of the signal), and C is the capacitance of the capacitor.

This represents the following phase vector (phasor) diagram, where a component in an AC circuit is represented as a vector having a real (resistive) value and an imaginary (reactive) value

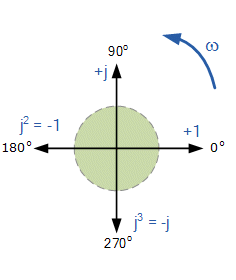
Several facts show from the above formula, The j-operator has a value equal to √-1, and represents a counter-clockwise rotation of 90o so successive 'rotations' of " j ", ( j x j ) will result in j having the following values of, -1, -j and +1.

As the j-operator is being used to indicate the counter-clockwise rotation of a vector, each successive rotation of " j ", j², j³ etc, will force the vector to rotate through a fixed angle of 90^o in a counter-clockwise direction as shown in the figure left.
Likewise, if the multiplication of the vector results in a -j operator then the phase shift will be -90^o, i.e. a clockwise rotation.

90^o rotation = j = √-1
180^o rotation = j² = -1
270^o rotation = j³ = j
360^o rotation = j⁴ = 1

The addition or subtraction of complex numbers is performed by adding or subtracting the real numbers and adding or subtracting the imaginary numbers. For example , if

A = x +jy and B = w + jz, then
A + B = (x + w) + j * (y + jz), and
A - B = (x - w) + j * (y - jz)

The multiplication of complex numbers follows more or less the same rules as for normal algebra along with some additional rules for the successive multiplication of the j-operator where: j2 = -1. S,

A * B = (x + jy) * (w + jz) = xw + jzx + jyw + j²yz = xw + j * (zx + yw) - yz = xw - yz + j * (zx + yw)

The division of complex numbers is a little more difficult to perform. The denominator is considered to be one half of the quadratic equation a² - b² =0. This resolves to (a + b) * (a - b) = 0. If b is an imaginary number then b² will be a real number. So multiplying the denominator by its conjugate pair, a process termed rationalising" will make the calculation possible. Let

A / B
=
4 + j1 / 2 + j3

Multiplying top and bottom by the conjugate of the denominatot, 2 - j3, gives

A / B
=
(4 + j1) * ( 2 - j3) / (2 + j3) * ( 2 - j3)
=
8 - j12 + j2 - j²3 / 4 -j6 + j6 - j²9
=
8 + 3 - j10 / 4 + 9
=
11 - j10 / 13

The resistance of an ideal capacitor is zero.
The reactance of an ideal capacitor, and therefore its impedance, is negative for all frequency and capacitance values. The negative sign arises from the fact that the voltage across a capacitor lags the current, as shown in a phasor diagram
The effective impedance (absolute value) of a capacitor is dependent on the frequency, and for ideal capacitors always decreases with frequency.

The voltage of an inductor leads the current by 90 degrees. The following equation is used for the impedance of an inductor:

Z_L = jωL

where Z_L is the impedance of the given inductor, ω is the angular frequency, and L is the inductance of the inductor. The conclusions that can be drawn from this formula: are

The resistance of an ideal inductor is zero.
The reactance of an ideal inductor, and therefore its impedance, is positive for all frequency and inductance values.
The effective impedance (absolute value) of an inductor is dependent of the frequency and for ideal inductors always increases with frequency.

Search Knowledge Base

Feedback

If you like our web site refer a friend.
Your friends name.	Your friends email address.
Your Name	Your Email Address