One of the most important issues in corporate finance is the magnitude of the equity risk premium. The risk premium is the incremental return that shareholders require from holding risky equities rather than risk-free securities. The risk premium drives future equity returns and is the key determinant of the cost of capital. A rule of thumb measure has been developed by Elroy Dimson, Paul Marsh and Mike Staunton at the London Business School, involving the return on risk free government bonds and anticipated dividend growth.
Investors have cause to ask what returns they can expect from equities, and what the future risk-reward trade-off is likely to be. Companies also need to answer this question in order to understand what returns their shareholders require from projects of differing risk. Regulators, too, need to know the cost of capital in order to set `fair' rates of return for regulated industries.

The notion that risk matters and that riskier investments should have a higher expected return than safer investments to be considered good investments is intuitive. Thus, the expected return on any investment can be written as the sum of the riskfree rate and an extra return to compensate for the risk. The disagreement, in both theoretical and practical terms, remains on how to measure this risk and how to convert the risk measure into an expected return that compensates for risk..

Risk is defined in terms of variance in actual returns around an expected return; thus, an investment is riskless when actual returns are always equal to the expected return. Also, risk has to be measured from the perspective of the marginal investor in an asset and that this marginal investor is well diversified. Therefore, the argument goes, it is only the risk that an investment adds on to a diversified portfolio that should be measured and compensated.
In fact, it is this view of risk that leads models of risk to break the risk in any investment into two components. There is a firm-specific component that measures risk that relates only to that investment or to a few investments like it and a market component that contains risk that affects a large subset or all investments. It is the latter risk that is not diversifiable and should be rewarded.

While all risk and return models agree on these fairly crucial distinctions, they differ when it comes to how measure this market risk. The following table summarises four models and the way each model attempts to measure risk.

	Asssumptions	Measure of Market Risk
The CAPM	There are no transactions costs or private information. Therefore, the diversified portfolio includes all traded investments, held in proportion to their market value.	Beta measured against this market portfolio.
Arbitrage pricing model (APM)	Investments with the same exposure to market risk have to trade at the same price (no arbitrage).	Betas measured against multiple (unspecified) market risk factors.
Multi-Factor Model	Same no arbitrage assumption	Betas measured against multiple specified macro economic factors.
Proxy Model	Over very long periods, higher returns on investments must be compensation for higher market risk.	Proxies for market risk, for example, include market capitalisation and Price/BV ratios.

ß_j = Beta of investment relative to factor j
Risk Premium_j = Risk Premium for factor j

Assuming that the riskfree rate is known, these models all require two inputs. The first is the beta or betas of the investment being analysed and the second is the appropriate risk premium(s) for the factor or factors in the model.

We would like to measure how much market risk (or non-diversifiable risk) there is in any investment through its beta or betas. As far as the risk premium is concerned, we would like to know what investors, on average, require as a premium over the riskfree rate for an investment with average risk, for each factor.
Consider the estimation of the beta and the risk premium in the capital asset pricing model. Here, the beta should measure the risk added on by the investment being analysed to a portfolio, diversified not only within asset classes but across asset classes. The risk premium should measure what investors, on average, demand as extra return for investing in this portfolio relative to the riskfree asset.

In practice, however, we compromise on both counts. We estimate the beta of an asset relative to the local stock market index, rather than a portfolio that is diversified across asset classes. This beta estimate is often subject to wild fluctuations (noisy) and a historical measure of risk. We estimate the risk premium by looking at the historical premium earned by stocks over default-free securities over long time periods.

These approaches might yield reasonable estimates in markets like the United States, with a large and diverisified stock market and a long history of returns on both stocks and government securities.
However, they yield meaningless estimates for both the beta and the risk premium in other countries, where the equity markets represent a small proportion of the overall economy and the historical returns are available only for short periods.

There is an alternative to estimating risk premiums that does not require historical data or corrections for country risk, but does assume that the market overall is correctly priced. Consider, for instance, a very simple valuation model for stocks.

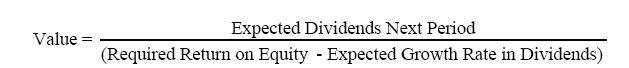
This is essentially the present value of dividends growing at a constant rate. Three of the four variables in this model can be obtained externally

• the current level of the market (i.e., value),
• the expected dividends next period and
• the expected growth rate in earnings and dividends in the long term.

To illustrate, assume that the current level of the S&P 500 Index is 900, the expected dividend yield on the index for the next period is 2% and the expected growth rate in earnings and dividends in the long term is 7%. Solving for the required return on equity yields the following:

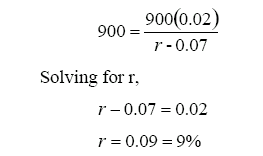
The advantage of this approach is that it is market-driven and current and it does not require any historical data. Thus, it can be used to estimate implied equity premiums

Given the history of the risk premium, how should investors seek to calculate such a value? The first step is to define the equity risk premium more exactly. It can be broken down into the following components:

• the dividend yield,
• plus the real dividend growth rate,
• plus or minus any change in the price/dividend ratio (the inverse of the dividend yield),
• minus the real risk-free interest rate.

The dividend yield comprised the vast bulk of the return. This was true across all the countries studied. Had investors consistently bought the highest-yielding quintile of equity markets over the past 112 years they would have earned an average nominal annual return of 13.3% compared with a return of just 5.4% for those buying the lowest-yielding quintile.
High-dividend markets have also performed best so far this century.

The importance of the dividend yield is ironic, given the lack of focus on the measure in most modern investment commentary. Many analysts argue that the dividend has been superseded by the share buy-back which (particularly in America) is a more tax-efficient way of returning cash to shareholders. But, although buy-backs reduce share capital, companies are also finding ways to add to it. Firms issue shares to pay for acquisitions, for example, or to reward executives through incentive schemes. Historically, net share issuance has been around 2% of total equity capital a year. This dilution of existing shareholders is part of the reason why real dividend growth has been so low, well below GDP growth.