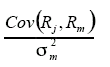The conventional approach for estimating the beta of an investment is a regression of the historical returns on the investment against the historical returns on a market index.
For firms that have been publicly traded for a length of time, it is relatively straightforward to estimate returns that an investor would have made on investing in stock in intervals (such as a week or a month) over that period. In theory, these stock returns on the assets should be related to returns on a market portfolio, i.e. a portfolio that includes all traded assets, to estimate the betas of the assets.
In practice, we tend to use a stock index, such as the S&P 500, as a proxy for the market portfolio, and we estimate betas for stocks against the index.

The standard procedure for estimating betas is to regress stock returns (R_j) against market returns (R_m) -

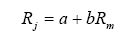
where

a = Intercept from the regression
b = Slope of the regression =

A statistic that emerges from the regression is the R squared (R²) of the regression. The statistical explanation of the R squared is that it provides a measure of the goodness of fit of the regression. The economic rationale is that it provides an estimate of the proportion of the risk of a firm that can be attributed to market risk; the balance (1 - R²) can then be attributed to firm-specific risk.

The final statistic worth noting is the standard error of the beta estimate. The slope of the regression, like any statistical estimate, may be different from the true value; and the standard error reveals just how much error there could be in the estimate. The standard error can also be used to arrive at confidence intervals for the 'true' beta value from the slope estimate.

The historical approach to estimating betas works only for assets that have been traded and have market prices. Private companies do not have a market price history. Consequently, we cannot estimate a regression beta for these companies. Nevertheless, we still need estimates of cost of equity and capital for these companies.
You might argue that this is not an issue because you do not value private companies but you will still be confronted with this issue even when valuing publicly traded firms.

Consider, for instance, the following scenarios.

• If you have to value a private firm for an initial public offering, you will need to estimate discount rates for the valuation.
• Even after a firm has gone public, there will be a period of time lasting as long as two years when there will be insufficient data for a regression.
• If you are called upon to value the division of a publicly traded firm that is up for sale, you will not have past prices to draw upon to run a regression.
• Finally, if your firm has gone through significant restructuring û divestitures or recapitalisation û in the recent past, regression betas become meaningless because the company itself has changed its risk characteristics.

Some analysts assume that discounted cash flow valuation is not feasible in these scenarios and use multiples. Others make assumptions about discount rates based upon rules of thumb.