
Is there more risk in investing in a Malaysian or Brazilian stock than there is in investing in the UK? The answer, to most, seems to be yes. That, however, does not answer the question of whether there should be an additional risk premium charged when investing in those markets.
Measuring Country Risk PremiumsIf country risk matters and leads to higher premiums for riskier countries, the obvious follow-up question becomes how we measure this additional premium. There are two approaches.
The first builds on default spreads on country bonds issued by each country whereas the second uses equity market volatility as its basis.
While there are several measures of country risk, one of the simplest and most easily accessible is the rating assigned to a country's debt by a ratings agency (S&P Moody's and BCA all rate countries). These ratings measure default risk (rather than equity risk), but they are affected by many of the factors that drive equity risk: the stability of a country's currency, its budget and trade balances and its political stability, for instance.
The other advantage of ratings is that they come with default spreads over the US treasury bond. For instance, the table below summarises the ratings and default spreads for Latin American countries on June 2000.
| Country | Rating | Typical Spread | Market Spread |
| Argentina | B1 | 450 | 433 |
| Bolivia | B1 | 450 | 469 |
| Brazil | B2 | 550 | 483 |
| Colombia | Ba2 | 300 | 291 |
| Ecuador | Caa2 | 750 | 727 |
| Guatemala | Ba2 | 300 | 331 |
| Honduras | B2 | 550 | 537 |
| Mexico | Baa3 | 145 | 152 |
| Paraguay | B2 | 550 | 581 |
| Peru | Ba3 | 400 | 426 |
| Uruguay | Baa3 | 145 | 174 |
| Venezuela | B2 | 550 | 571 |
- Ratings are foreign currency ratings from Moody's.
- Typical spreads are estimated by looking at the default spreads on bonds issued by all countries with this rating and are over and above a riskless rate (U.S. treasury or German Euro rate).
- Market spread measures the spread difference between dollar-denominated bonds issued by this country and the U.S. treasury bond rate.
The market spreads measure the difference between dollar-denominated bonds issued by the country and the U.S. treasury bond rate. While this is a market rate and reflects current expectations, country bond spreads are extremely volatile and can shift significantly from day to day. To counter this volatility, we have estimate typical spreads by averaging the default spreads of all countries in the world with the specified rating over and above the appropriate riskless.
These spreads tend to be less volatile and more reliable for long term analysis.
Analysts who use default spreads as measures of country risk typically add them on to both the cost of equity and debt of every company traded in that country. For instance, the cost of equity for a Brazilian company, estimated in U.S. dollars, will be 4.83% higher than the cost of equity of an otherwise similar U.S. company.
If we assume that the risk premium for the United States and other mature equity markets is 5.51%, the cost of equity for an average Brazilian company can be estimated as follows (with a U.S. Treasury bond rate of 5% and a beta of 1.2).
Cost of equity = Riskfree rate + Beta *(U.S. Risk premium) + Default Spread= 5% + 1.2 (5.51%) + 4.83% = 16..34%
In some cases, analysts add the default spread to the U.S. risk premium and multiply it by the beta. This increases the cost of equity for high beta companies and lowers them for low beta firms.
Default spreads measure the risk associated with bonds issued by countries and not the equity risk in these countries. Since equities in any market are likely to be more risky than bonds, you could argue that default spreads understate equity risk premiums.
Assume that all companies in a country are equally exposed to country risk. Thus, for Brazil, with an estimated country risk premium of 9.69%, each company in the market will have an additional country risk premium of 9.69% added to its expected returns. For instance, the cost of equity for Aracruz Cellulose, a paper and pulp manufacturer listed in Brazil, with a beta of 0.72, in US dollar terms would be (assuming a US treasury bond rate of 5% and a mature market (US) risk premium of 5.59%):
Expected Cost of Equity = 5.00% + 0.72 (5.51%) + 9.69% = 18.66%To convert this dollar cost of equity into a cost of equity in the local currency, all that we need to do is to scale the estimate by relative inflation. To illustrate, if the BR inflation rate is 10% and the U.S. inflation rate is 3%, the cost of equity for Aracruz in BR terms can be written as:
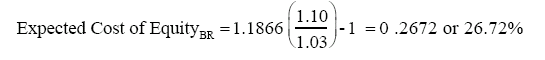
Assume that a company's exposure to country risk is proportional to its exposure to all other market risk, which is measured by the beta. For Aracruz, this would lead to a cost of equity estimate of:
Expected Cost of Equity = 5.00% + 0.72 (5.51% + 9.69%) = 15.94%This approach does differentiate between firms, but it assumes that betas which measure exposure to market risk also measure exposure to country risk as well. Thus, low beta companies are less exposed to country risk than high beta companies.
The most general, and our preferred approach, is to allow for each company to have an exposure to country risk that is different from its exposure to all other market risk.
We will measure this exposure with lambda and estimate the cost of equity for any firm as follows:

How is lambda best estimated? Commodity companies which get most of their revenues in US dollars by selling into a global market should be less exposed than manufacturing companies that service the local market.
Using this rationale, Aracruz, which derives 80% or more of its revenues in the global paper market in US dollars, should be less exposed than the typical Brazilian firm to country risk. Using a lambda of 0.25, for instance, we get a cost of equity in US dollar terms for Aracruz of:

Expected Return = 5% + 0.72 (5.51%) + 0.25 (9.69%) =11.39%
© Copyright 1998-1999 GOOD2USE